Hình lăng trụ là gì? Lăng trụ đều là gì? Tính chất và bài tập?

1. Hình lăng trụ là gì?

Hình lăng trụ là một dạng hình đa diện có đặc điểm gồm hai mặt đáy là hai đa giác bằng nhau và nằm trên hai mặt phẳng song song. Mỗi mặt bên của hình lăng trụ là một hình bình hành và các cạnh bên là song song và bằng nhau. Hơn nữa, hai mặt đáy của hình lăng trụ có thể là hình vuông, hình chữ nhật, hình tam giác và các hình đa giác khác.

2. Công thức tính thể tích và diện tích hình lăng trụ:

Một trường hợp đặc biệt của hình lăng trụ là hình hộp, khi đáy của nó là một hình bình hành.

Thể tích hình lăng trụ bằng diện tích của mặt đáy nhân với chiều cao hình lăng trụ hoặc là khoảng cách giữa hai mặt đáy.

V = B.h

Trong đó:

– B là diện tích mặt đáy của hình lăng trụ

– h là chiều cao của của hình lăng trụ

– V là thể tích hình lăng trụ

Diện tích xung quanh hình lăng trụ

Diện tích xung quanh hình lăng trụ bằng chu vi đáy hoặc tổng diện tích các mặt bên nhân với chiều cao của hình lăng trụ.

Sxq = 2p.h

Trong đó:

– p là nửa chu vi đáy

– h là chiều cao của hình lăng trụ

– Sxq là diện tích xung quanh của hình lăng trụ

Diện tích toàn phần hình lăng trụ

Diện tích toàn phần hình lăng trụ bằng tổng diện tích hai đáy và tổng các diện tích xung quanh.

Stp = 2S + Sxq

Trong đó:

– S là diện tích đa giác ở mặt đáy

– Sxq là diện tích xung quanh của hình lăng trụ

– Stp là diện tích toàn phần của hình lăng trụ

3. Hình lăng trụ đều là gì?

Hình lăng trụ đều là một hình lăng trụ đứng có đáy là một đa giác đều. Nghĩa là, hình lăng trụ đứng có các cạnh bên vuông góc với mặt đáy.

Ví dụ: Các hình lăng trụ đều bao gồm hình lăng trụ tam giác đều, hình lăng trụ tứ giác đều, hình lăng trụ ngũ giác đều và hình lăng trụ lục giác đều.

Tính chất:

– Hai mặt đáy là hai đa giác đều bằng nhau, vì vậy các cạnh đáy cũng sẽ bằng nhau.

– Các cạnh bên vuông góc với mặt đáy.

– Các mặt bên của hình lăng trụ là các hình chữ nhật.

4. Các hình lăng trụ đều thường gặp:

– Hình lăng trụ tam giác đều là hình lăng trụ có hai mặt đáy là hai hình tam giác đều.

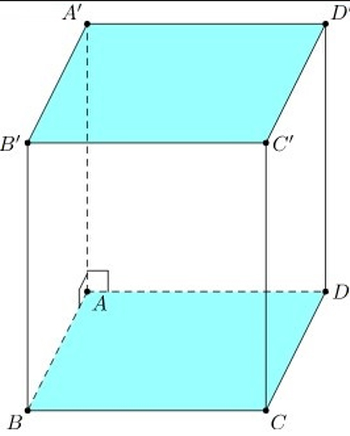
– Hình lăng trụ tứ giác đều là hình lăng trụ đều có hai mặt đáy là hình vuông.

– Hình lăng trụ ngũ giác đều là hình lăng trụ đều có hai mặt đáy là hình ngũ giác.

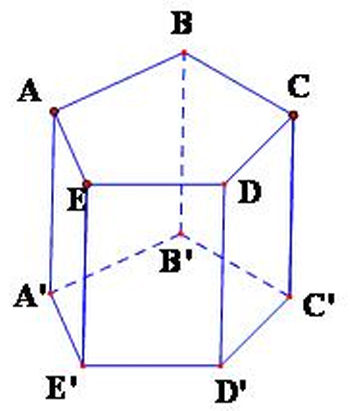
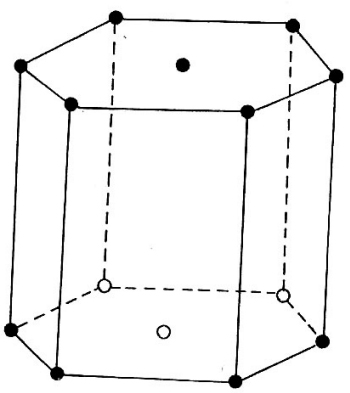
– Hình lăng trụ lục giác đều là hình lăng trụ đều có hai mặt đáy là hình lục giác.

5. Bài tập vận dụng:

5.1. Bài tập trắc nghiệm:

Câu 1: Hình lăng trụ đều được xác định bởi:

A. Một đa diện hai chiều đều với hai đa giác đều là hai đỉnh đầu mút và các cạnh bên song song và đồng đều nhau.

B. Hai mặt đáy được tạo thành từ hai hình đa giác, còn các mặt bên là các hình chữ nhật có cùng kích thước.

C. Hai mặt đáy là hai đa giác đều và cân nhau, trong khi các mặt bên là các hình chữ nhật đồng nhất kích thước.

D. Hai mặt đáy là hai đa giác đều bằng nhau, mặt bên là các hình chữ nhật.

Hướng dẫn giải: Đáp án C

Bể cá này có kích thước chiều dài là 2 lần kích thước chiều rộng. Tính dung tích lớn nhất của bể cá có thể chứa được là 1,50 m³.

B. 1,15 m³

C. 1,23 m³

D. 1,45 m³

Hướng dẫn giải: Đáp án A

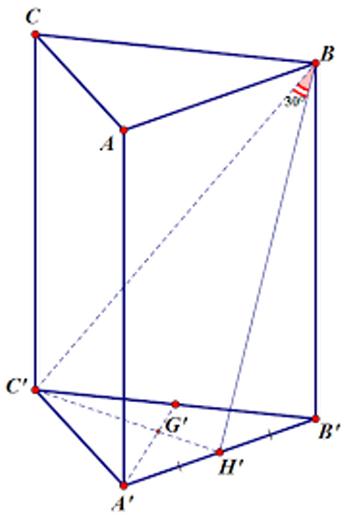
Chúng ta cần tính thể tích của khối lăng trụ ABC.A'B'C', với cạnh đáy ABC có độ dài a. Điểm A' có hình chiếu vuông góc lên mặt phẳng (ABC) và trùng với tâm O của đường tròn ngoại tiếp tam giác ABC. Bên cạnh đó, cạnh A'O cũng có độ dài bằng a.

Kết quả: a³/12

B. (a³√3)/ 6

C. (a³√3)/ 12

D. a³/2

Hướng dẫn giải: Đáp án C

Câu 4: Biết tất cả các cạnh bằng a. Tính thể tích của khối lăng trụ tam giác đều đó.

A. V = √3a³/6

B. V= √3a³/4

C. V = √3a³/3

D. V= √2a³/4

Hướng dẫn giải: Đáp án B

Câu 5: Cho một khối lăng trụ có diện tích đáy bằng 4a² và có chiều cao bằng a. Tính thể tích của khối lăng trụ đã cho theo a.

A. V = 4a³

B. V = a³

C. V = 2a²

D. 1/2a²

Hướng dẫn giải: Đáp án A.

Câu 6: Một hình bát diện đều có các mặt bên là hình gì?

A. Hình tam giác đều

B. Hình vuông

C. Hình chữ nhật

D. Hình tam giác cân

Hướng dẫn giải: Đáp án A

5.2. Bài tập tự luận:

Bài tập 1: Bạn được cho một hình lăng trụ có đáy là hình tam giác vuông với hai cạnh góc vuông lần lượt là 6 và 7 đơn vị và chiều cao là 8 đơn vị. Hãy tính thể tích của hình lăng trụ đó.

Hướng dẫn giải:

Diện tích đáy tam giác của hình lăng trụ là: S = ( 6. 7 )/ 2 = 21

Thể tích hình lăng trụ đó là: V = S. h = 21. 8 = 168.

Kết luận: Thể tích của hình lăng trụ đã cho là 168.

Bài tập 2: Tính thể tích của hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh bằng 10 và chiều cao AA' bằng 5.

Hướng dẫn giải:

Kẻ đường cao AH của tam giác ABC.

Vì tam giác ABC là tam giác đều nên H trở thành trung điểm của BC.

=> BH = CH = BC / 2 = 10/ 2 = 5

Vì tam giác ABH vuông tại H nên theo định lý Pytago ta có: AH = 5√75

Diện tích đáy hình lăng trụ là: SABC = ( AH.BC )/ 2 = 5√(75)

Thể tích của hình lăng trụ tam giác đều là: V = S. h = SABC. AH = 5√75. √75 = 375.

Kết luận: Vậy, thể tích của hình lăng trụ tam giác đều ABC.A’B’C’ là 375.

Đề bài yêu cầu tìm chiều cao của hình lăng trụ có mặt đáy là một hình tam giác vuông có cạnh góc vuông lần lượt là 3 và 6. Thông tin đã cho là thể tích của hình lăng trụ là 72.

Diện tích đáy hình lăng trụ là: S = ( 3. 6 )/ 2 = 9

Chiều cao của hình lăng trụ đó là: h = V/ S = 72/ 9 = 8

Kết luận: Chiều cao AH của tam giác đều ABC là 4.

Hướng dẫn giải:

Theo đề bài ta có:

Diện tích tam giác ABC là: SABC = V/ h = 90/ 3 = 30

Vì tam giác ABC là tam giác đều mà AH là đường cao nên H là trung điểm của BC.

Gọi tam giác đều ABC có cạnh bằng a.

=> BH = CH = 1/2BC = a/2

Vì tam giác ABH vuông tại H, theo định lý Pytago ta có: AH = a√(3/4)

Ta có: SABC = ( AH. BC )/ 2 = 30 => AH. BC = 60 <=> a√(3/4). a = 60

=> a = √80 => AH = √60

Kết luận: Vậy tam giác ABC có chiều cao AH bằng √60

Bài tập 5: Đề cho một hình lăng trụ ABC.A’B’C’ có đáy là tam giác ABC. Đường cao AH của tam giác ABC biết có độ dài 3, độ dài cạnh đáy BC bằng 4, và thể tích của hình lăng trụ là 42. Yêu cầu tính chiều cao của hình lăng trụ.

Diện tích tam giác ABC là: SABC = ( AH. BC )/ 2 = ( 3. 4 )/ 2 = 6

Chiều cao của hình lăng trụ ABC.A’B’C’ là: h = V/ SABC = 42/ 6 = 7

Kết luận: Chiều cao của hình trụ là 7.

Bài tập 6: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại A. Được biết cạnh AB có độ dài là 4, thể tích của hình lăng trụ là 36 và chiều cao là 6. Hãy tính độ dài cạnh AC.

Hướng dẫn giải:

Diện tích đáy tam giác ABC là: SABC = V/ h = 36/ 6 = 6

Vì tam giác ABC vuông tại A mà diện tích của tam giác bằng 6 nên ta có:

SABC = ( AB. AC )/ 2 = 6 => AC = 12/ AB = 12/ 4 = 3

Kết luận: Cạnh AC của tam giác ABC có độ dài là 3.

Bài tập 7: Cho hình lăng trụ ABC.A’B’C’ trong đó đường cao AH của đáy tam giác ABC. Biết rằng độ dài đường cao AH là 3, độ dài cạnh BC là 4 và thể tích của hình lăng trụ đã cho là 24. Hãy tính chiều cao của hình lăng trụ đã cho và độ dài cạnh BC'.

Hướng dẫn giải:

Diện tích đáy của hình lăng trụ đã cho là: SABC = ( 3. 4 )/2 = 6

Chiều cao của hình lăng trụ được cho là: h = V/ SABC = 24/ 6 = 4 => AA’ = BB’ = CC’ = 4

Vì tam giác BCC’ vuông tại C, ta áp dụng định lý Pythagoras như sau: (BC’)2 = (BC)2 + (CC’)2 = 32 BC’ = √(32)

Kết luận: Vậy lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 5, thể tích của khối lăng trụ đã cho là bao nhiêu?

Đáp án:

Áp dụng công thức: V = a2 x √3/4 x h

Khi tất cả cạnh của lăng trụ đều có độ dài 3, chiều cao của nó cũng là 3. Điều này được biết đến từ tính chất của hình lăng trụ tam giác đều, trong đó chiều cao là độ dài của cạnh bên.

Vì vậy, thể tích của lăng trụ là: V = 52 x √3/4 x 5 = (125√3)/4

Ta có hình lăng trụ đứng ABC.A’B’C’ với đáy ABC đều có cạnh bằng a và chu vi của mặt bên ABB’A’ là 6a. Cần tính thể tích của khối lăng trụ ABC.A’B’C’.

Đáp án:

Chúng ta cần nhận thức rằng để tính được thể tích V, đề bài đòi hỏi thêm thông tin về chiều cao h.

Vì mặt bên ABB'A' có chu vi bằng 6a theo tính chất của hình lăng trụ tam giác đều,

2 x (a + h) = 6a → h = 2a

Vậy áp dụng công thức thể tích V = a2 x √3/4 x h = a3 x √3/2

Bài tập 10: Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 5. Diện tích xung quanh lăng trụ đã cho bằng bao nhiêu?

Đáp án:

Áp dụng công thức: Stp = Sxq + 2 x Sđ = 3 x a x h + 2 x (√3)/4 x a2

Ở đây khi các cạnh bằng 5 thì chiều cao h = 5.

Do đó Stp = 3 x a2 + 2 x (√3)/4 x a2 = (3 + 2(√3)/4) x a2